Betrachten wir die Funktion $f(x,y)=x^3-3xy^2$. Das folgende Bild stellt diese Funktion grafisch dar.

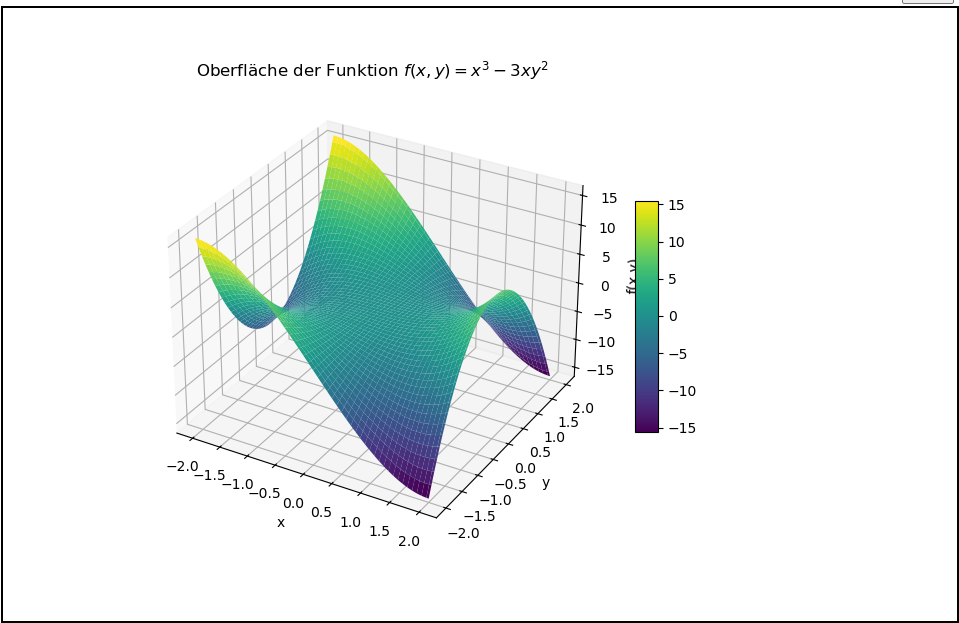
Überlege: Der Gradient steigt stets in die Richtung des steilsten Anstiegs einer Funktion. Wenn Du eine Murmel auf diese Fläche legst, so wird sie nach unten  in die entgegengesetzte Richtung rollen

Berechnung des Gradienten

Der Gradient von $f$ ist $\nabla{f} = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}) = (3x^2-3y^2, -6xy)$. Das dadurch definierte Gradientenvektorfeld hatten wir bereits hier betrachtet! Vergleiche es mit dem Graph der Funktion!

Experimentiere:

Schau Dir den Graphen und das zugehörige Vektorfeld des Gradienten für andere Funktionen an - wo steigt der Graph besonders steil an, wohin zeigt der Gradient dort? Ändere dazu die Definition der Funktion in Zeile 7 nach Belieben.