Wir betrachten die Funktion $f(x,y):\mathbb{R}^2 \rightarrow \mathbb{R}^2$, die durch $f(x,y)=(3x^2 - 3y^2, -6xy)$ definiert ist. Diese Funktion ordnet jedem Punkt $(x,y)$ der Ebene $\mathbb{R}^2$ einen Vektor zu. Wird dieser Vektor im Punkt $(x,y)$ eingezeichnet, so ergibt sich folgendes Bild.

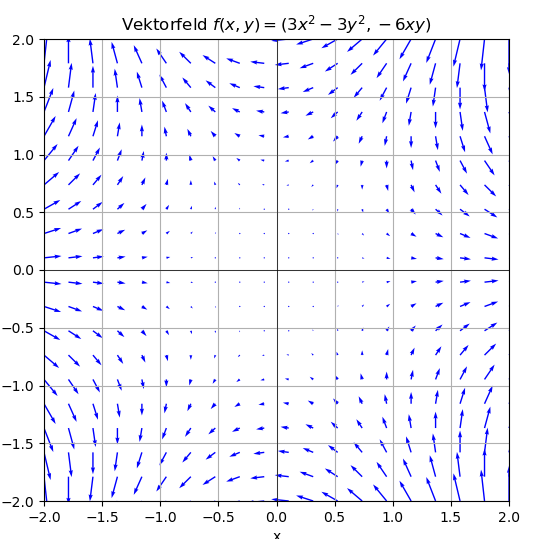
Möchtest Du mehr Vektorfelder sehen? Dann klicke hier und ersetze die Funktion $f$ in Zeile 6 durch eine Funktion Deiner Wahl.